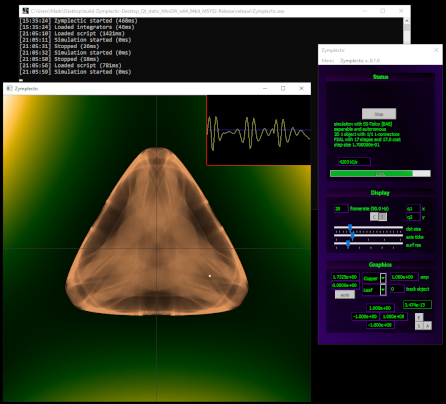
Zymplectic project
High performance numerical platform for Hamiltonian systems
In dedication of scientific endeavours on and applications of explicit symplectic integrators, Zymplectic is an installation free, c/c++ based, high performance scientific computation toolbox featuring an excessive assortment of dynamical systems to be simulated by the single largest collection of symplectic partioned Runge-Kutta and Runge-Kutta-Nyström methods.| Zymplectic 0.11.1 - 2024.02.03 | Download links |
|---|---|
| Windows x86-64 | Zymplectic v.0.11.1 win64 gcc Zymplectic v.0.11.1 win64 clang |
| Linux x86-64 | Currently unavailable |


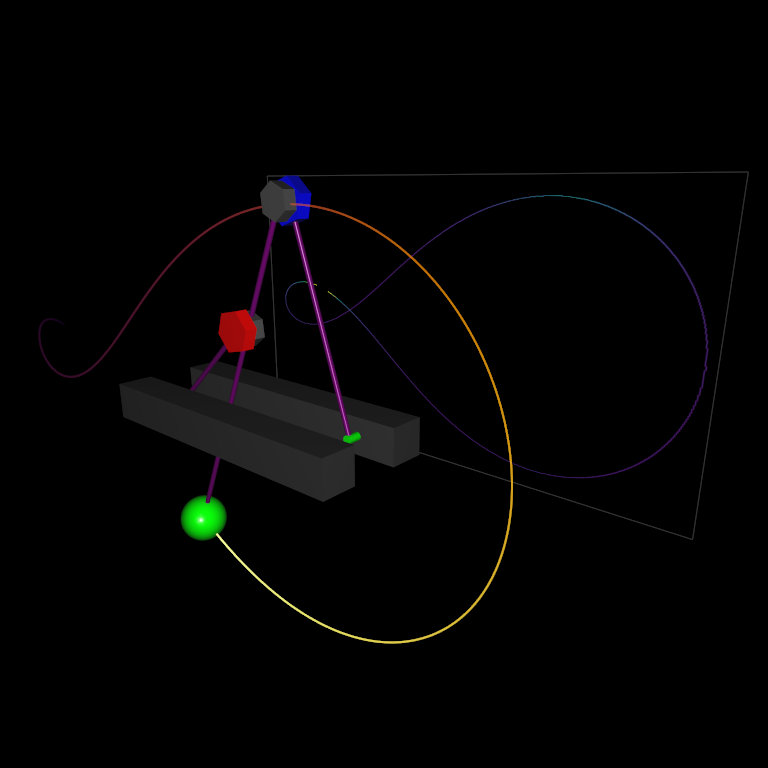

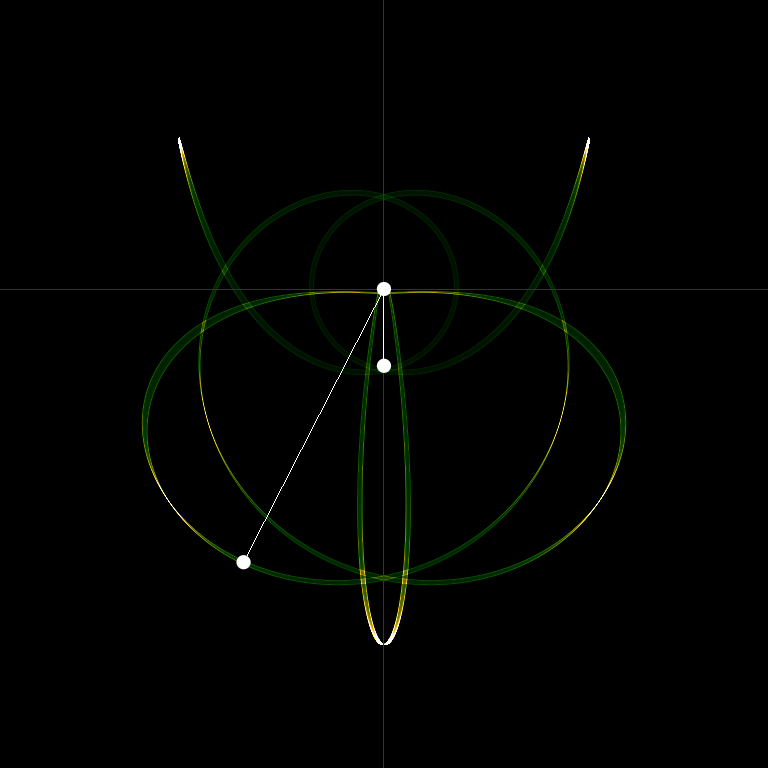
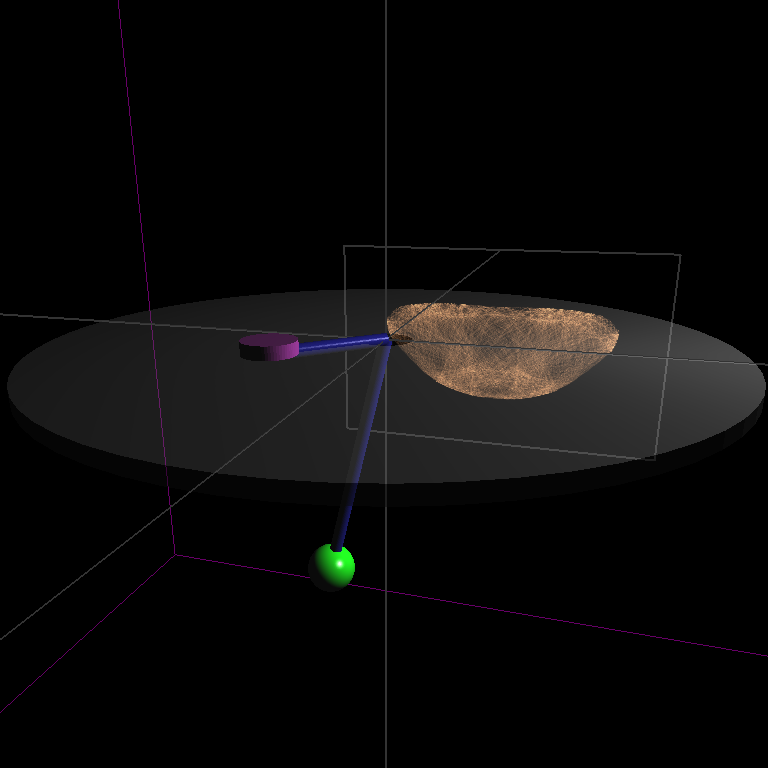
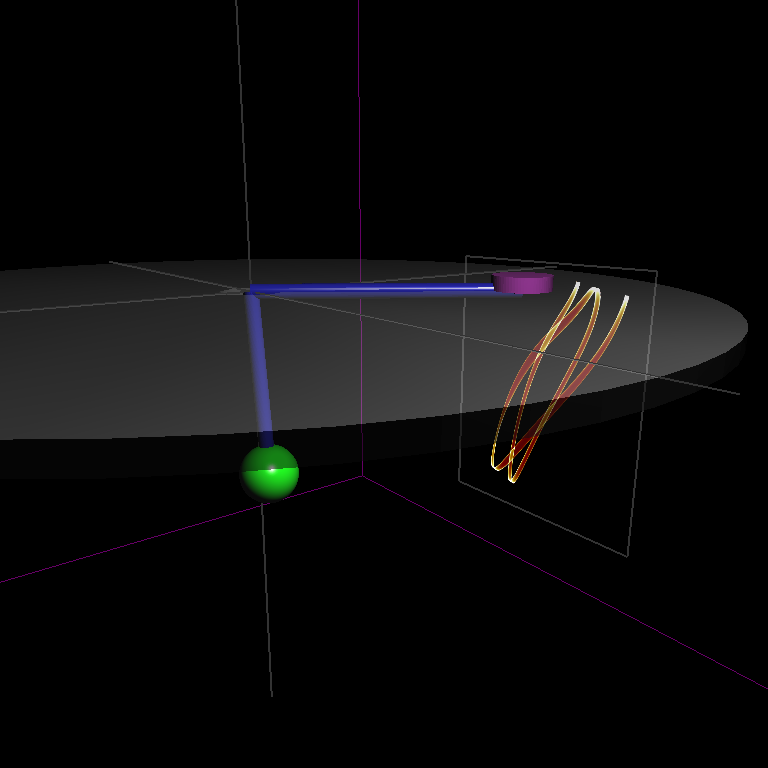











Introduction
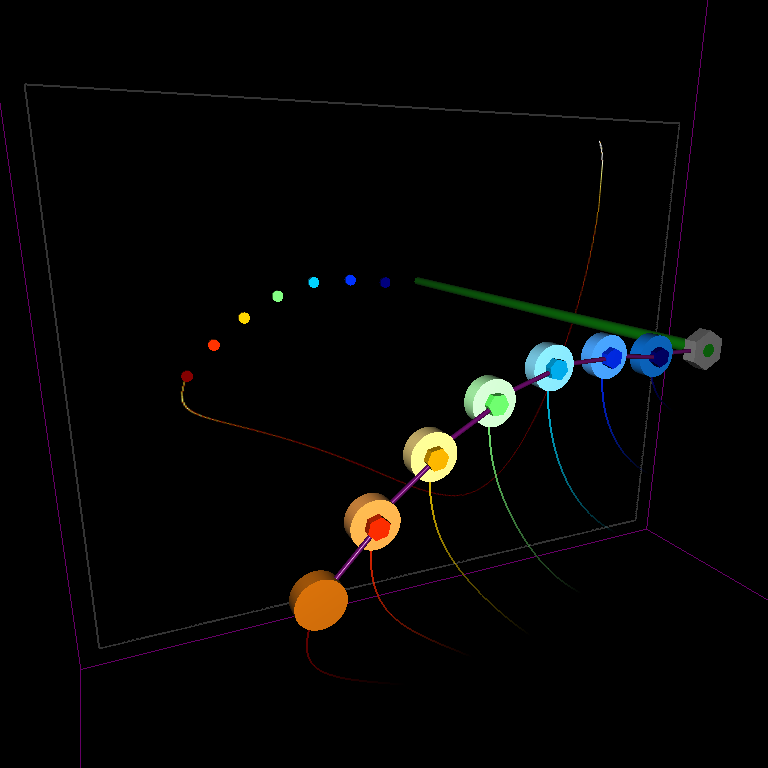
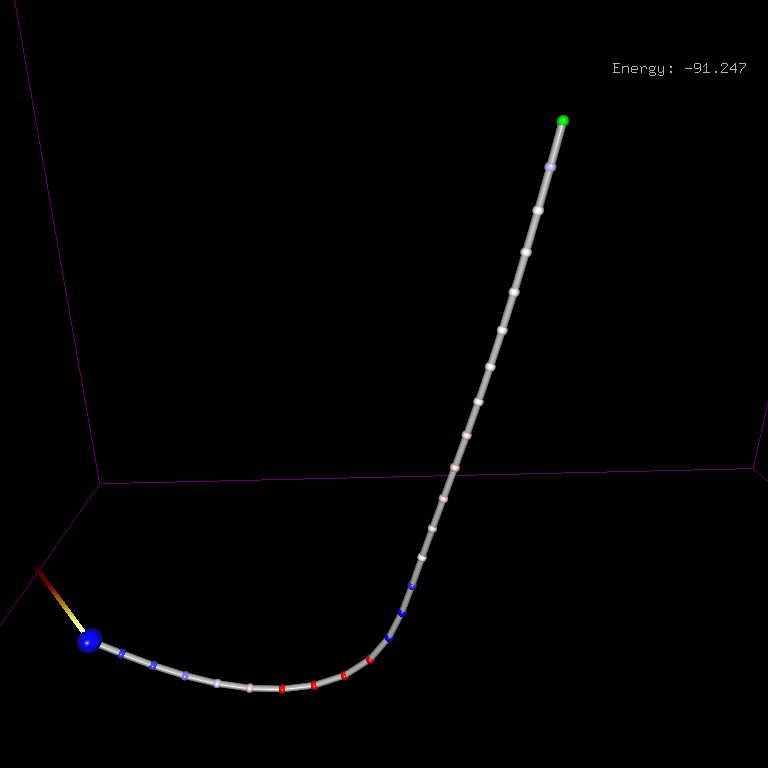
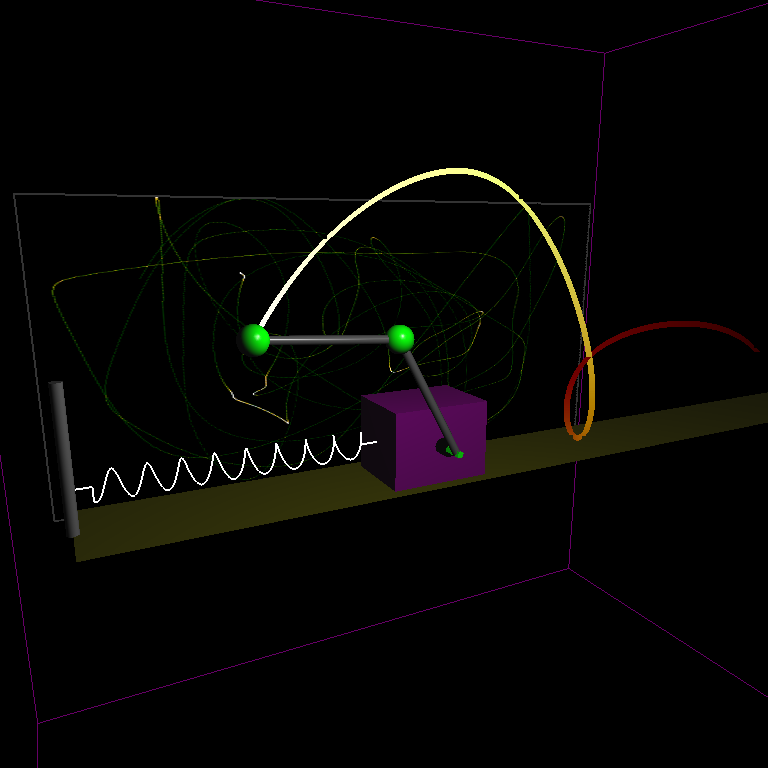
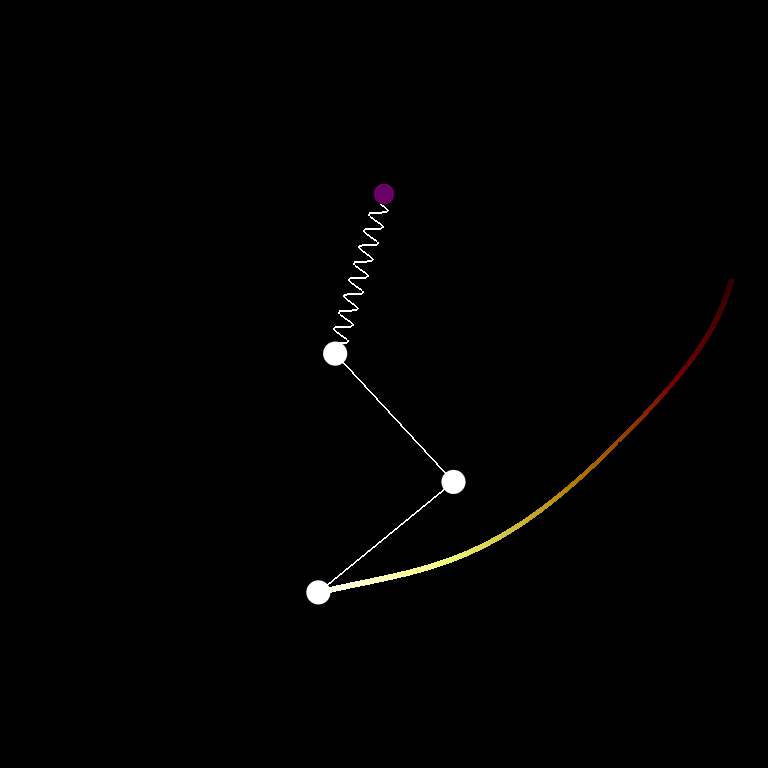
SIs preserve the phase-space volume exactly and counteract dissipation of the initial Hamiltonian as opposed to well-acclaimed non-symplectic Runge-Kutta methods. SIs are widely used for long-time numerical integration in the fields of celestial mechanics, accelerator physics, molecular dynamics, and quantum chemistry, and in particular any form of state space analyses that are particularly vulnerable to dissipative errors.
The symplectic Euler method (first order) and the leapfrog method (second order) in spite of their poor accuracy are among the most acclaimed SIs, and are often used without the users' awareness of the symplectic properties.
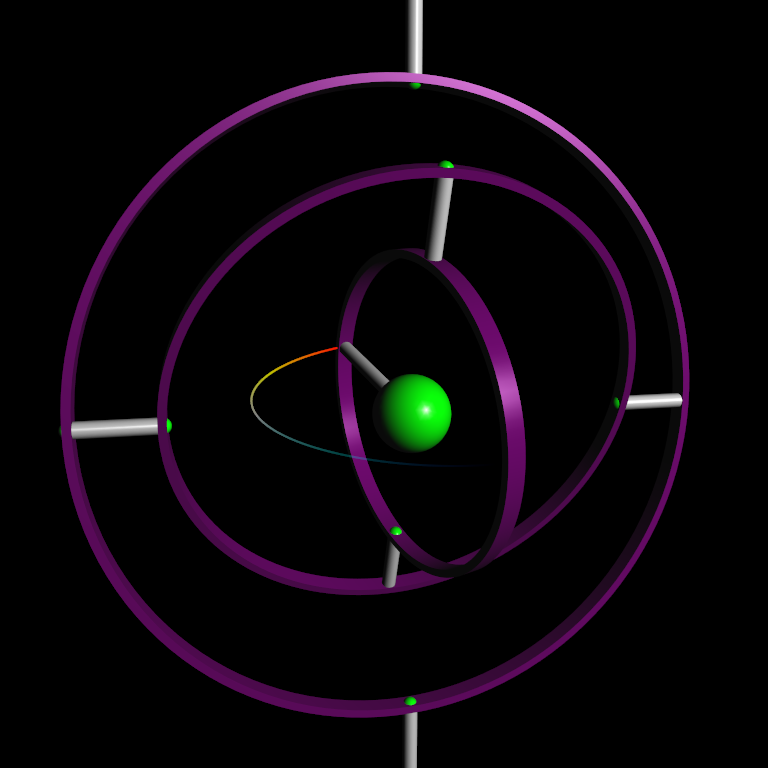
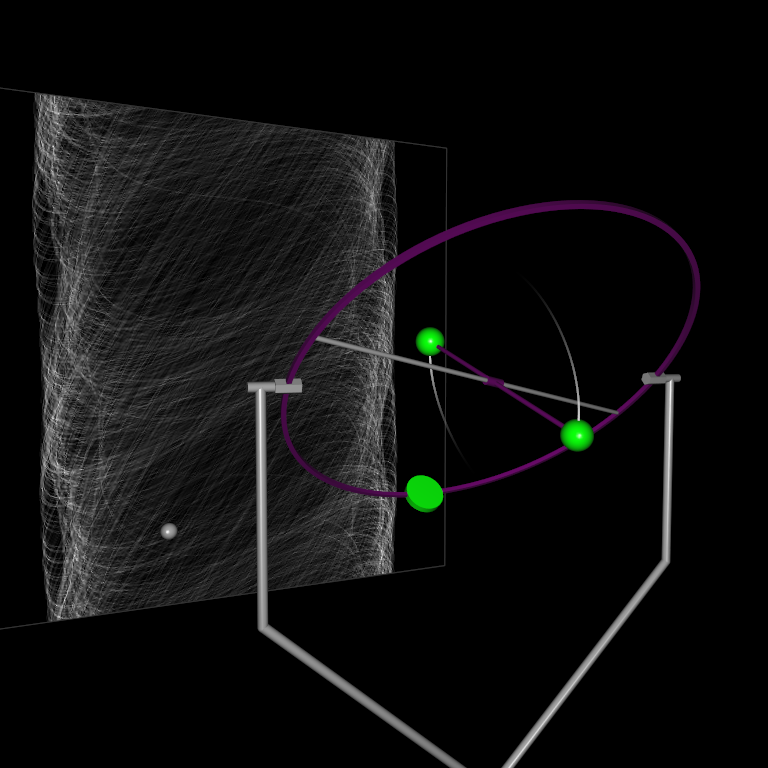
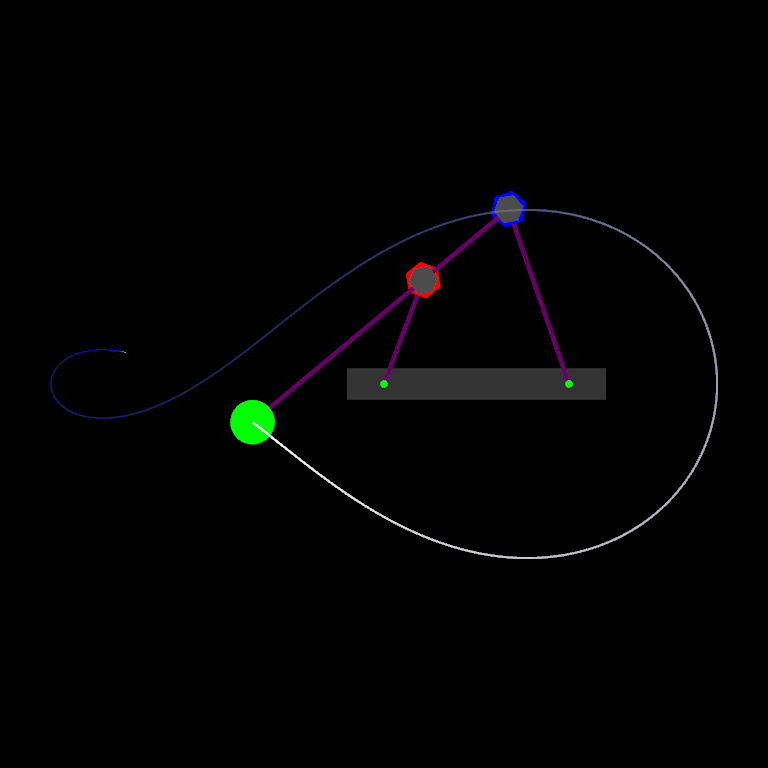
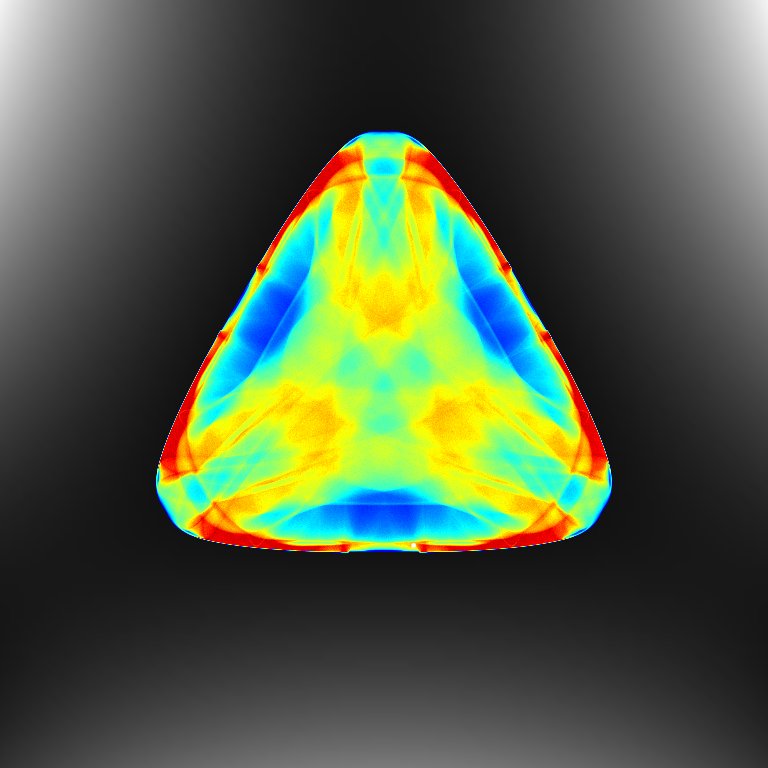
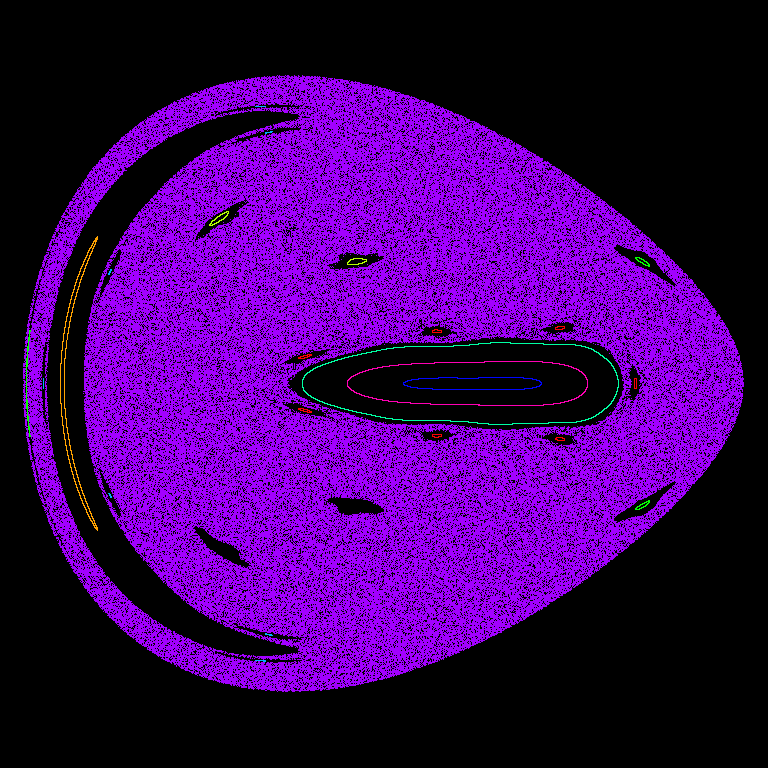
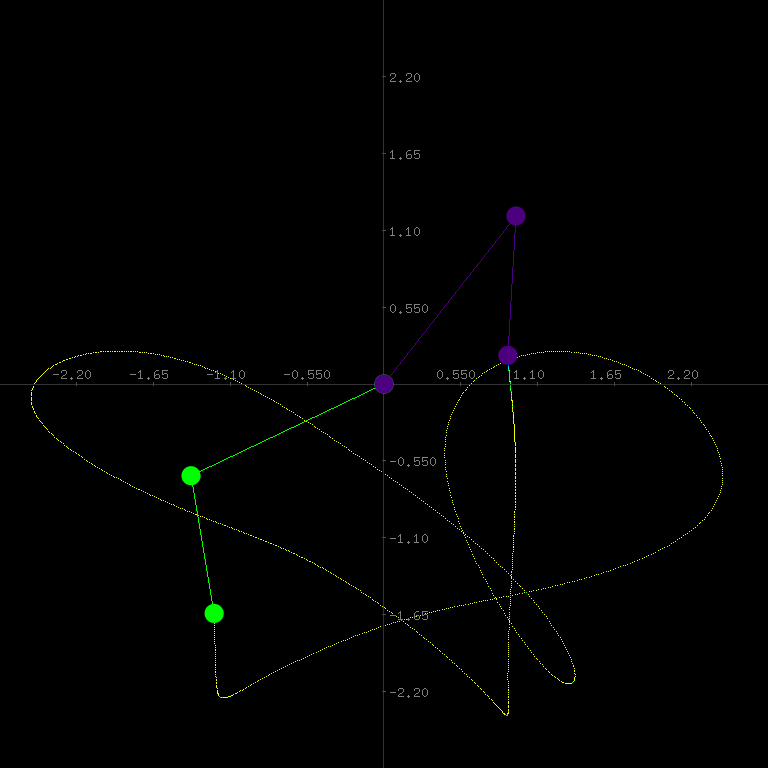
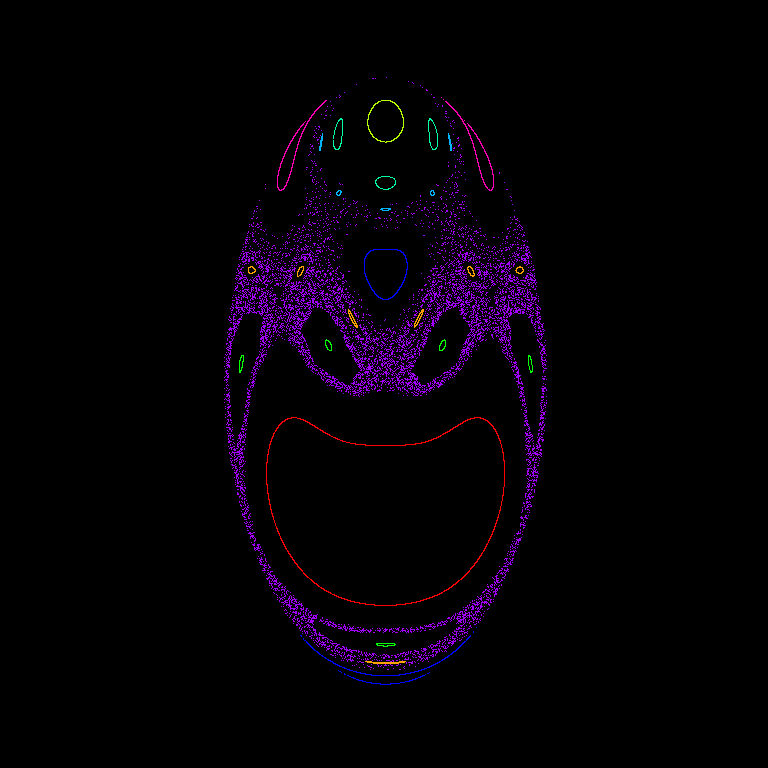
The Hamiltonian is one of the qualitative physical properties of autonomous dynamical systems that is preserved throughout the numerical integration (see demo, left mouse to start simulation):
Applications
In addition to their common application, SIs may also be applied to systems where T or V depend explicitly on time, that are the so-called non-autonomous systems where the Hamiltonian is generally not conserved. $$H = T(p,t)+V(q,t)$$ While explicit system integrators are primarily intended for separable Hamiltonian systems it has been shown that they can be applied to non-separable systems which can not be separated into two terms T(p) and V(q) or in other words that T or V depend irreducibly on both q and p, and without loss of generality may or may not depend explicitly on time:
$$H = f(p,q,t)$$ for any sufficiently smooth function f. Finally, SIs while possibly waiving some symplectic properties, can have their use extended to a wide range of differential equations such as ordinary differential equations that may not be governed by a Hamiltonian.The Zymplectic project
Showcases
- 1: The Two-body problem
- 2: Trajectories of Hamiltonian systems
- 3: Integrator (autonomous and separable)
- 4: The quadrupole mass spectrometer
- 5: The Kapitza pendulum
- 6: The double pendulum
- 7: Benchmark: Fifth order integrators
- 8: Soft boundary billiards
- 9: Spherical pendulum (Euler angles)
- 10: Spherical pendulum (stereographic projection)
Zymplectic features
- Prebuilt GUI with no setup or dependencies
- Bundled with GCC or clang to dynamically compile c++ code
- More than 70 examples to be simulated with a single click
- More than 100 SPRK and RKN integrators
- Built-in Kahan summation for reducing truncation errors
- Practical 2D/3D OpenGL-based UI with interactive features
- Benchmarking to identify the best methods for a given system
- Wide scope supporting conventional separable Hamiltonian systems, but also non-separable, non-autonomous and non-holonomic systems
Ease of use
//example implementation of Hénon-Heiles system
#include "math.h"
const double lambda = 1.0;
double _q_init[] = {0.3,0.0}; //initial position
double _p_init[] = {0.0,0.4}; //and momentum
double energy_H(Arg) { //Hamiltonian (optional)
return lambda*q2*(q1@2 - q2@2/3.0) + 0.5*(q1@2 + q2@2 + p1@2 + p2@2);
} //Zymplectic supports the power operator @
void dH(Arg) { //Hamilton's equations
dq1 = q1 + lambda*2*q1*q2;
dq2 = q2 + lambda*(q1@2 - q2@2);
dp1 = p1;
dp2 = p2;
}
void main() {
Z.H(energy_H,dH,0);
}Further reading
- Survey on Symplectic Integrators. Markiewicz, D. 1999, Preprint Univ. California at Berkeley get article
- Splitting Methods for Non-autonomous Hamiltonian Equations. Blanes, Sergio and Moan, P. C. 1, 2001, Journal of Computational Physics, Vol. 170, pp. 205-230 get article
- Composition constants for raising the orders of unconventional schemes for ordinary differential equations. Kahan, William and Li, Ren-Cang. 219, 1997, Mathematics of Computation, Vol. 66, pp. 1089-1099 get article
- Fourth-order symplectic integration. Forest, Etienne and Ruth, Ronald D. 1, 1990, Physics D, Vol. 43, pp. 105-117 get article
- Construction of higher order symplectic integrators. Yoshida, Haruo. 5-7, 1990, Physics Letters A, Vol. 150, pp. 262-268 get article
- New families of symplectic splitting methods for numerical integration in dynamical astronomy. Blanes, Sergio, et al. s.l. : Applied Numerical Mathematics, June 2013, Applied Numerical Mathematics, Vol. 68, pp. 58-72 get article
- High precision symplectic integrators for the Solar System. Farrés, Ariadna, et al. 2, 2013, Celestial Mechanics and Dynamical Astronomy, Vol. 116, pp. 141-174 get article
- High order symplectic integrators for perturbed Hamiltonian systems. Lasker, Jacques and Robutel, Philippe. 1, 2001, Celestial Mechanics and Dynamical Astronomy, Vol. 80, pp. 39-62 get article
- Optimized fifth order symplectic integrators for orbital problems. Tselios, Kostas and Simos, T.E. 1, 2013, Revista Mexicana de Astronomía y Astrofísica, Vol. 49, pp. 11-24 get article